最近連假在家除了看劇耍廢之外，研究了之前在 Leecode 上解迴文的相關題目時，看到的演算法解法

一般來說在處理迴文時，直覺的中心擴展法或是 DP 的方式都需要 $O(N^2)$ 的時間，但利用該演算法卻可以在線性時間 $O(N)$ 內完成

這個演算法是由 Manacher Glenn 在 1975 年發現，在線性時間內算出所有迴文字串的方法

Manancher 的論文發表在 ACM
(1975), “A new linear-time “on-line” algorithm for finding the smallest initial palindrome of a string”

後人基於他的發現，進而發展出找出最長迴文子字串 LPS (Longest Palindromic Substrings) 的演算法，就叫做 Manacher’s Algorithm

一開始只看程式碼完全看不懂為什麼，上網找了幾個解說網頁搭配看，自己在紙上推敲後才恍然大悟，真的是很聰明的方法，分享給想要耗損精力(?)的各位

概念

在線性時間內在一個字串中找出所有迴文的演算法，主要是用來解決 LPS (Longest Palindromic Substrings) 的問題

Manacher 的方法的前置作業是會在每個字串之間插入一個不相干的符號，比如用 #，然後利用一個正整數陣列計算每個位置的迴文半徑，也就是以該位置為中心的迴文長度

假設給定字串為 “aabaaca”

插入符號後的 = “#a#a#b#a#a#c#a#”

紀錄 length 的 table 會是這樣

string # a # a # b # a # a # c # a #
radius 0 1 2 1 0 5 0 1 2 1 0 3 0 1 0

以 “#a#a#b#a#a#” 這組子字串為例，以 b 為中心點的迴文半徑長度(#a#a#)就是 5

也可以發現 length 雖然紀錄的是半徑，但也是以該字母為中心迴文的實際長度(扣掉符號後)

最後根據這個 table 紀錄的數值我們就能得出最長迴文的長度

這裡有個很酷的 Manacher’s Algorithm 動畫可以搭配參考

中心擴展

先來看怎麼從一般的方式判定一個字串是迴文並且計算長度的方法: 中心擴展法，這也是原本直覺在一個字串中找迴文的方法

  1. 從中心點向左右擴展
  2. 比對左右的字串
  3. 字母一樣就判定是迴文，count++ (由於我們是要紀錄半徑，所以只需要 count + 1)
1
2
3
4
int count = 0;
while(s.charAt(i - 1 - count) == s.charAt(i + 1 + count)) {
  count++;
}

這時候可以發現插入符號的好處，就是當字串長度是偶數時，除以二後的中心點會在符號上，方便我們直接進行擴展比對，而且在單個字母的例子中，透過左右兩旁的符號計算半徑時也能得出他的迴文長度是 1 (單個字母也是迴文)

鏡像特性

Manacher’s Algorithm 之所以能線性時間內完成的核心，就是完美利用了的迴文的鏡像(mirror)特性

在 Manacher 運用的鏡像方法中需要界定一個中心值 C，與一個界定右邊半徑範圍的值 R

我們以上述例子 “#a#a#b#a#a#c#a#” 的子字串 “#a#a#b#a#a#” 為例，參考以下我粗製的示意圖

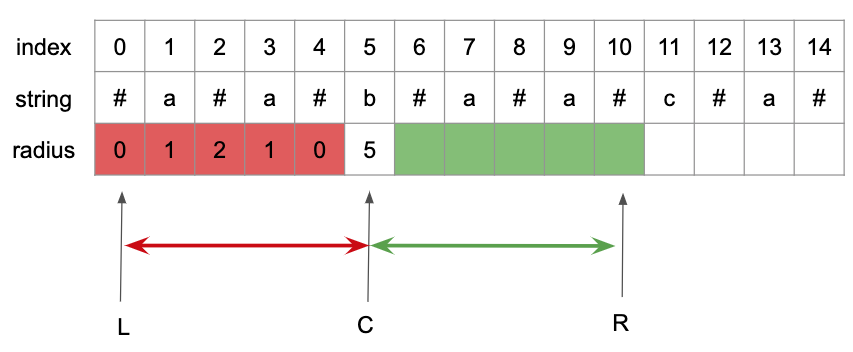
假設我們已經求完 s[5] = 5，這時候 R 會在 5 + s[5]，也就是 index 10 的位置，而 C 就會是在 index 5 的地方

這時候可以發現在 R 以內的 radius，可以用鏡像的方式直接得到，原理就是在以 s[5] 為中心的迴文中，在範圍 R 內右半部的數值都會等於左半部

1
2
3
4
5
6
s[6] = s[4]
s[7] = s[3]
s[8] = s[2]
s[9] = s[1]
s[i] = s[mirror_i]
C = 5

我們可以推出

mirror_i = C - (i - C) = 2C - i

只要運用這個鏡像原理，不斷更新 R 與 C，與更新右半部分的數字，就能在線性時間內完成

特殊情況

要注意的是利用鏡像原理也會有幾個特殊情況需要處理，碰到特殊情況時就得回去使用中心擴展法

Case 1: i >= R

當 i >= R 時，不能用鏡像，因為目前這個就字母不在可以使用鏡像範圍內，所以我們得用中心擴展求出 radius

Case 2: mirrorIndex <＝ 原字串首字母

r[mirrorIndex] 等於第一個符號的時候，使用鏡像可能會出錯

e.g. “cbcbcb”

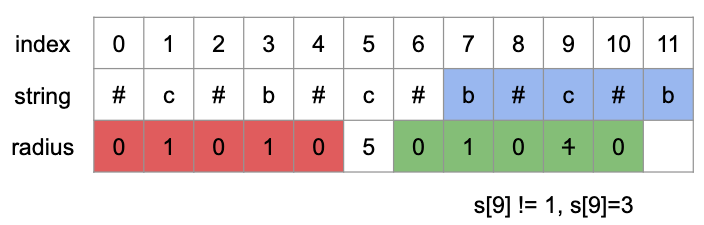
2021/09/25 修正

  • 這裡的 s[3] & s[7] 圖做錯了，radius 是 3，原圖已經遺失，只能文字更新了

在 s[5] 的地方為 C，s[10] 的地方為 R

s[9] 雖然在 R 的範圍內，以鏡像方式求得會是 s[9] = s[1] = 1，但事實上 s[9] 不是 1，而是 3

會發生這種情況是因為 s[1] 是原本字串的頭了，在 s[5] 用中心擴展時無法考慮 s[1] 的更左邊的情形了，所以在考慮 s[9] 的情況時會忽略它右邊的子字串也有可能與左邊的子字串互為迴文的情形

這時候我們在 s[9] 就得用中心擴展法才能得到正確的 radius

Case 3: i + s[mirror_i] > R

這個情況的意思是 i 的位置上，如果用鏡像得到的數值加上目前的 index i 是會超過 R，那代表這個數值也不正確，需要用中心擴展法

跟 case 2 可以說是有點類似，同樣是彌補鏡像法沒有 cover 到的情形，也就是右方子字串變化的特殊情況

e.g. “cbcbcbcbb”

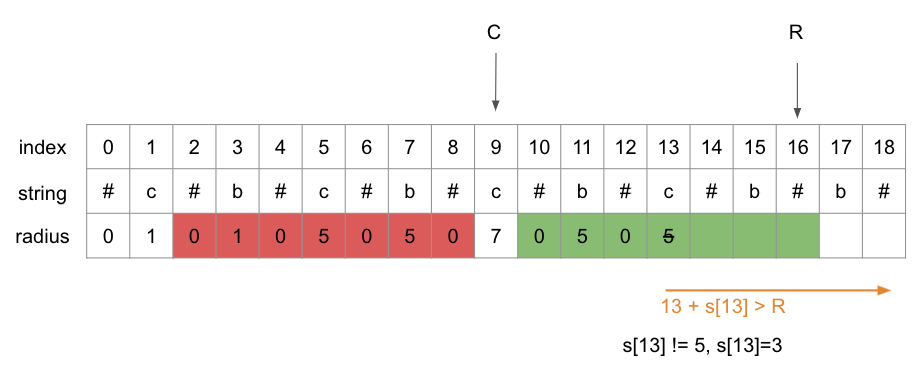
謝謝 Ryan 在一樓的詳細說明

這時候的中心擴展法可以只考慮 R 以外的範圍，因為迴文特性，只要在 R 範圍內的字串，其 radius[i] 至少會等於 R - i

頭尾再插入不同符號

為了方便中心擴展法在計算 count 時不會遇到超出邊界的情況，通常會在字串頭尾再插入另外兩種符號

比如在字串首加入$，尾巴加入^，e.g. “$#a#a#b#a#a#c#^”

這樣我們在做 s[i - 1 - count] == s[i + 1 + count] 的比對時，當有情況是迴文長度會碰到左邊界或右邊界，就會直接因為符號不相等而結束迴圈，省去我們判斷是否 out of bound 的情形

程式碼

2021/09/25 更新更好讀的程式碼
2021/09/30 更新 case 3

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
// Manacher's Algorithm
public void palindromicSubstrings(String s) {
    String symbolString = insertSymbolInString(s);
    int n = symbolString.length();
    System.out.println(symbolString);

    int radius[] = new int[n];
    int C = 0, L = 0, R = 0;

    for (int i = 2; i < n - 1; i++) {
        int mirrorIndex = C * 2 - i;
        // special cases, using central expand to get radius
        if (mirrorIndex <= 2 || i >= R || i + radius[mirrorIndex] >= R) {
            if (mirrorIndex >= 0 && i + radius[mirrorIndex] >= R) {
                // We can just do central expanding among unknown range
                radius[i] = R - i;
            } else {
                radius[i] = 0;
            }
            while (symbolString.charAt(i - radius[i] - 1) == symbolString.charAt(i + radius[i] + 1)) {
                radius[i]++;
            }
            // update C and R
            C = i;
            L = i - radius[i];
            R = i + radius[i];
        } else {
            radius[i] = radius[mirrorIndex];
        }
     }
    System.out.println(Arrays.toString(radius));
}
    
private String insertSymbolInString(String s) {
    String symbolString = "$#";
    for (int i = 0; i < s.length(); i++) {
        symbolString += s.charAt(i) + "#";
    }
    return symbolString + "^";
}

複雜度

雖然看似有兩層迴圈，但經過一些複雜的證明(?)的時間複雜度是接近 $O(N)$，原因是因為裡面的那層 While 並不會超出 R，而用鏡像原理處理的那些位置不會用到 While

2021/09/25 更新

  • 準確來說是有機會到達 $O(N)$ 複雜度，Worst case 的情況下還是接近 $O(N^2)$
  • 感謝一樓 Ryan 大大補充，實測後確實是 $O(N)$，速度比一般的中心擴展或是 DP，快了近一倍！

空間複雜度是 $O(N)$

最長迴文子字串

首先要解決的是如何透過紀錄的 radius 長度，回推字串的開頭位置

(i - radius[i]) / 2 = 迴文字串在原字串的開頭位置

我們算出 radius table 後只要簡單紀錄 maxIndex，跑一次迴圈就能知道最長迴文的長度

1
2
3
4
5
6
7
8
9
10
11
int maxIndex = 1;

// [1 ~ n - 1] 的範圍是因為頭尾是用來界定邊界的不同符號，不需要計算到
for (int i = 1; i < n - 1; i++) {
    if (radius[i] > radius[maxIndex]) {
        maxIndex = i;
    }
}
int startIndex = (maxIndex - radius[maxIndex]) / 2;

String LPS = s.substring(startIndex, startIndex + radius[maxIndex]);

但如果是要算出所有迴文有幾組呢？

如何計算總共有幾個迴文

例子

一樣用上面提到過的例子來舉例，”aabaaca”

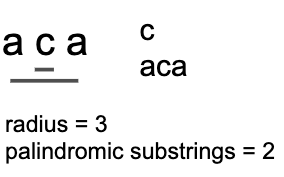
先看子字串 “aabaa” 的情形，以 b 為中心的 radius 是 5，考慮以 b 為中心向左右擴散，拆解這個迴文字串內有幾組子字串是迴文，總共會有 “b”, “aba”, “aabaa” 三組

以下附上三個拆解的示意圖幫助理解

注意：radius 的計算如同上面闡述的一樣，是包含符號而算的值

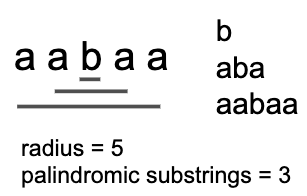
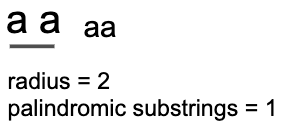
以此類推

以此類推我們可以觀察到

1
2
3
4
aca (radius = 3) => c, aca => 2 palindromic substrings
aabaa (radius = 5) => b, aba, aabaa => 3 palindromic substrings
aabccbaa (radius = 8) => cc, bccb, abccba, aabccbaa => 4 palindromic substrings
aabcbcbaa (radius = 9) => b, cbc, bcbcb, abcbcba, aabcbcbaa => 5 palindromic substrings

So all palindromic substrings at each position of radius array is (radius + 1) / 2

所以只要在跑 radius table 的迴圈內，把每個位置上代表的迴文中會有幾組迴文子字串，全部加總即可得到答案

1
2
3
4
int count = 0;
for (int i = 1; i < n - 1; i++) {
     count += (radius[i] + 1) / 2; 
}

真的覺得以前的數學家都很有時間鑽研最佳化…XD，身為凡人真心佩服啊，希望這篇有幫助到人，複雜的演算法是很難單看程式碼去理解背後原理的，當初在看的時候真的一頭霧水，建議拿筆跟紙真的演練一下，即使是亂塗也能助於大腦理解