概念

新增、刪除、修改一個字元算做一步的話，最少需要做幾步？就是Edit distance的概念

先來說明Edit distance的實例

output edit distance of two input strings:

Example 1

1
2
3
4
5
// input
ab
ab
// output
0

Example 2

1
2
3
4
5
// input
short
ports
// output
3

Example 3

1
2
3
4
5
// input
editing
distance
// output
5

2016 舊文章

心得

Edit distance的演算法我還不是了解的很透徹為什麼要這樣做，其中二維陣列的填表需要透過圖解來幫助理解，自己在紙上實際跑一次會比較有概念

假設以short vs ports這個例子來說，一開始填好第一行第一列，藍色箭頭是代表表格填入的順序

edit1

仔細看演算法，會發現每次決定該格數值都是參考該格的上、下、左上的數值，這些數值就是insertion、deletion、match、mismatch定義的值

edit2

拉出來的四格中

  • A+1 = insertion
  • B+1 = deletion
  • C+1 = mismatch
  • C = match

2020 再更新

終於在 2020 的今天，想到要來還債了哈哈

P.S. 因為舊文附的 pseudo code 我覺得沒有比較好懂，先移除，上面保留概念跟以前做的圖XD

在 2016 年時我是先用 Google Blog 開始記錄文章，前陣子整理發現原來我一直沒有關閉我的 Google Blog (現在已經關掉惹)，然後有人在這篇文下面提問上面第二個例子為什麼是 3 步，回顧了下這篇才驚覺我當初沒有完全理解，為了補齊漏洞，就來更新下

BTW，原來 Edit Distance 在 Leetcode 是 Hard 等級的問題！難怪我覺得比 LCS 複雜，所以一時想不出來為什麼也很正常！(喂)

先來看為什麼第二個例子是 3

1
2
3
4
5
// input
short
ports
// output
3

最小編輯距離是算出兩個字串之間的差異

考慮字串順序，做新增、刪除、編輯各算為一步的話，”short” 最少需做幾步才會變成 “ports”

  1. 修改 “s” 為 “p” : “short” -> “phort”
  2. 刪除 “h” : “phort” -> “port”
  3. 增加 “s” : “port” -> “ports”

最少會需要 3 步

第三個例子也是一樣的概念

1
2
3
4
5
// input
editing
distance
// output
5
  1. 刪除 “e” : “editing” -> “diting”
  2. 增加 “s” : “diting” -> “disting”
  3. 修改 “i” 為 “a” : “disting” -> “distang”
  4. 修改 “g” 為 “c” : “distang” -> “distanc”
  5. 增加 “e” : “distanc” -> “distance”

如果第一步先選擇修改 e 變 d，就會多一步，但編輯距離要的是最少步數，所以其他可行的編輯方法就不是最終答案

動態規劃

這題看起來很複雜，但還是回歸 DP 在處理字串比對上的二維陣列去看就會比較清楚

一樣以字串 A = “short” 與字串 B = “ports” 的例子來看

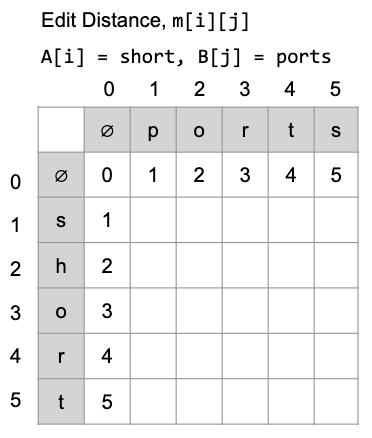
分析初始狀態

m[0][j] 的位置上，代表的是 A 空字串要做多少步會變成 B[j]，所以每一格都需要用新增的方式

m[i][0] 的位置上，代表的是 A[i] 字串要做多少步才會變成 B 空字串，所以每一格都需要用刪除的方式

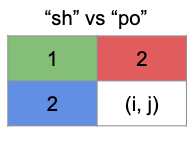
比如 m[0][2] 指的就是在字串 A 中 (0-0) 的位置代表的字串，要編輯多少步才能變成字串 B 中 (0-2) 代表的字串，也就是 “” vs “po”，所以 m[0][2] = 2，因為需要作兩次新增

m[2][0] 指的是在字串 A 中 (0-2) 的位置代表的字串 “sh” 要編輯多少步才能變成字串 B (0-0) 位置代表的字串 “”，就是做兩次刪除

以此類推就能先填好第一行與第一列

分析子問題

可以先來分析看看在每一格做比對的話會是什麼情形，藉此去觀察規則

1
2
3
4
5
6
7
8
9
10
11
12
13
14
m[1][1] = "s" vs "p" -> A[1] != B[1]
字母不相等，所以勢必需要做 1 次編輯

因為需要累績編輯距離，所以我們要考慮AB兩個字串在前一輪字串然後配對

會有三種組合，選有最小編輯距離的那一個，組合如下

1. "s" vs " " -> m[1][0]
2. " " vs "p" -> m[0][1]
3. " " vs " " -> m[0][0]
m[1][1] = MIN(m[1][0], m[0][1], m[0][0]) + 1 
        = MIN(1, 1, 0) + 1
        = 0 + 1 
        = 1

以此類推

1
2
3
4
5
6
7
8
m[2][1] = "sh" vs "p" -> A[2] != B[1]
1. "sh" vs " " -> m[2][0]
2. "s" vs "p" -> m[1][1]
3. "s" vs " " -> m[1][0]
m[2][1] = MIN(m[2][0], m[1][1], m[1][0]) + 1
        = MIN(2, 1, 1) + 1
        = 1 + 1 
        = 2
1
2
if A[i] != B[j]
  m[i][j] = MIN(m[i][j - 1], m[i - 1][j], m[i - 1][j - 1]) + 1

於是我們就可以根據規則填表格到以下這個狀態

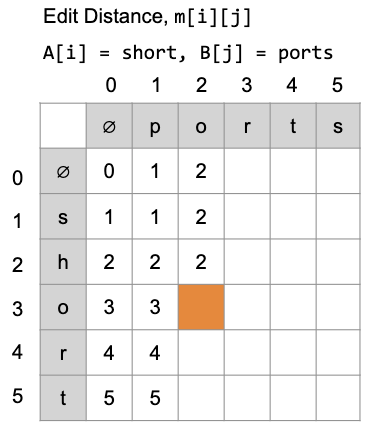
上面是 A[i] != B[j] 的情況，來看看如果是 A[i] == B[j] 的情況會是如何

1
2
3
4
5
6
m[3][2] = "sho" vs "po" -> A[i] == B[j]
因為字母一樣，所以我們可以直接參考 AB 兩字串在這個字母的前一次的組合的值

"sh" vs "p" = m[2][1] = 2

m[3][2] = m[2][1]
1
2
if A[i] == B[j]
  m[i][j] = m[i - 1][j - 1]

按照規則填入數值，最後 m[A.length][B.length] 就是 A、B 兩個字串的最小編輯距離

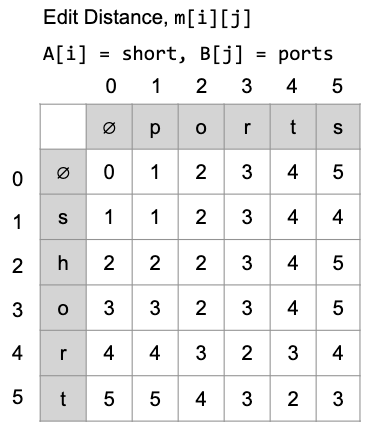
程式碼

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
class Solution {
    public int minDistance(String word1, String word2) {
        // DP
        int m = word1.length();
        int n = word2.length();
        int matrix[][] = new int[m + 1][n + 1];
        
        // init
        for (int i = 0; i <= m; i++) {
            matrix[i][0] = i;
        }
        for (int j = 0; j <= n; j++) {
            matrix[0][j] = j;
        }
        
        // choose minimum edit distance from the neighbors
        for (int col = 1; col <= n; col++) {
            for (int row = 1; row <= m; row++) {
                if (word1.charAt(row - 1) == word2.charAt(col - 1)) {
                    matrix[row][col] = matrix[row - 1][col - 1];
                } else {
                    matrix[row][col] = Math.min(
                       matrix[row - 1][col], 
                       Math.min(
                          matrix[row][col - 1], 
                          matrix[row - 1][col - 1])) + 1;
                }
            }
        }
        return matrix[m][n];
    }
}

相鄰三格的意義

在 review 這篇時卡住我一整天的概念，是在 Edit Distance 的 DP 表格中，目標位置 (i, j) 與相鄰三格的意義

在是以 col 放來源字串 A，row 放目標字串 B 的情形下，Edit distance 的 pattern 會是

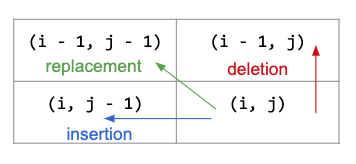
乍看之下有點不明白

後來先按照上述那樣分析子問題，才漸漸明白為什麼是這樣定義

箭頭的走向很重要，所以我一定要特別畫出來說明

直接舉例來看，上面表格 m[2][2] 的位置拉出來

replacement

綠色格就是回到 “s” vs “p” 的情況來看時，在 (i, j) 的位置上做什麼動作

此時其實是 “p” vs “p”，因為在 “s” vs “p” 時，是做了 1 步編輯，修改 “s” 為 “p”

所以此時 “sh” vs “po” 的情況實際是 “ph” vs “po”

修改 “h” 變 “o” -> 就是 “po” vs “po”

在這格累計總步數就是 2 步

deletion

紅色格就是回到 “s” vs “po” 的情況來看時，在 (i, j) 的位置上做什麼動作

此時其實是 “po” vs “po”，因為在 “s” vs “po” 的情況下，做了 2 步編輯，修改 “s” 為 “p”，跟新增 “o”

所以此時 “sh” vs “po” 的情況實際是 “poh” vs “po”

刪除 “h” 變成 “po” vs “po”

在這格累計總步數會是 3 步

insertion

藍色格就是回到 “sh” vs “p” 情況下來看時，在 (i, j) 的位置上做什麼動作

此時其實是 “p” vs “p”，因為在 “sh” vs “p” 的情況下，是做了 2 步編輯，取代 “s” 為 “p”，刪除 “h”

所以此時 “sh” vs “po” 的情況實際是 “p” vs “po”

為什麼不是 “ph” vs “po” 呢，原因是 “h” 已經被刪除了

這格需要花點時間理解，因為 “sh” vs “po”，回到 (i, j - 1)， “sh” vs “p”，來源字串 “sh” 並沒有變，所以會被在 (i, j - 1) 的編輯動作影響

新增 “o” 變成 “po”

再複習心得

事實證明，以前沒花時間理解全的，以後還是要花時間補全阿

推薦 YouTube 上不錯的講解影片，(是美式英文不是印度英文不要擔心)，但他 Row & Col 的順序跟我相反，概念上是一樣的，只是他沒特別講解新增、修改、刪除那三格為什麼是那樣

其實這題的新增、修改、刪除的 pattern 不用特別記，主要還是分析子問題去頗析字串組合就能推出條件了，我反而認為直接看這個 pattern 根本不知道在幹嘛XD，也有可能我還是理解力不夠

上面相鄰 pattern 的背後原因是我自己推敲的，有缺失的話，路過的大德們再好心留言告訴我吧